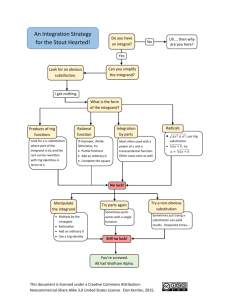
Example: the limit of start fraction start square root x end square root minus 2 divided by x minus 4 end fraction as x approaches 4 can be rewritten as the limit of start fraction 1 divided by start square root x end square root + 2 end fraction as x approaches 4, using conjugates and cancelling. Example: limit of start fraction x squared minus x minus 2 divided by x squared minus 2 x minus 3 end fraction, as x approaches negative 1 can be reduced to the limit of start fraction x minus 2 divided by x minus 3 end fraction as x approaches negative 1, by factoring and cancelling. If you obtained option D, try rewriting the limit in an equivalent form. Example: limit of start fraction x squared minus x minus 2 divided by x squared minus 2 x minus 3 end fraction, as x approaches negative 1. Option D: f of a = start fraction 0 divided by 0 end fraction. Example: limit of x squared as x approaches 3 = 3 squared = 9. Option C: f of a = b, where b is a real number.
Inspect with a graph or table to learn more about the function at x = a. Example: the limit of start fraction 1 divided by x minus 1 end fraction as x approaches 1.
Option B: f of a = start fraction b divided by 0 end fraction, where b is not zero. Evaluating f of a leads to options B through D. A flow chart has options A through H, as follows.